Linear Regression is one of the easiest and most powerful techniques used in machine learning to predict values. It’s widely used in areas like finance, marketing, health, real estate, and more, basically anywhere you want to predict a number (like salary, price, marks, etc.).

What Is Linear Regression?

Linear Regression is a technique that shows the relationship between two or more variables. One of the variables is what we want to predict (called the dependent variable), and the others are the inputs or features we use to make that prediction (called independent variables).It helps us draw a straight line through the data that best fits the pattern. This line can then be used to predict values.

• Dependent Variable (y): This is what you’re trying to predict. For example, house price.
• Independent Variable (x): This is the input or factor that affects the prediction. For example, square footage.
• Slope (m): Shows how much y changes for every 1 unit change in x.
• Intercept (c): The value of y when x is 0 (where the line crosses the y-axis).

The Equation: y = mx + c

This is the basic equation for simple linear regression (one independent variable).

• y: Predicted value (dependent variable)
• m: Slope of the line
• x: Input value (independent variable)
• c: Intercept (value of y when x = 0)

Here is the diagram illustrating the Linear Regression equation

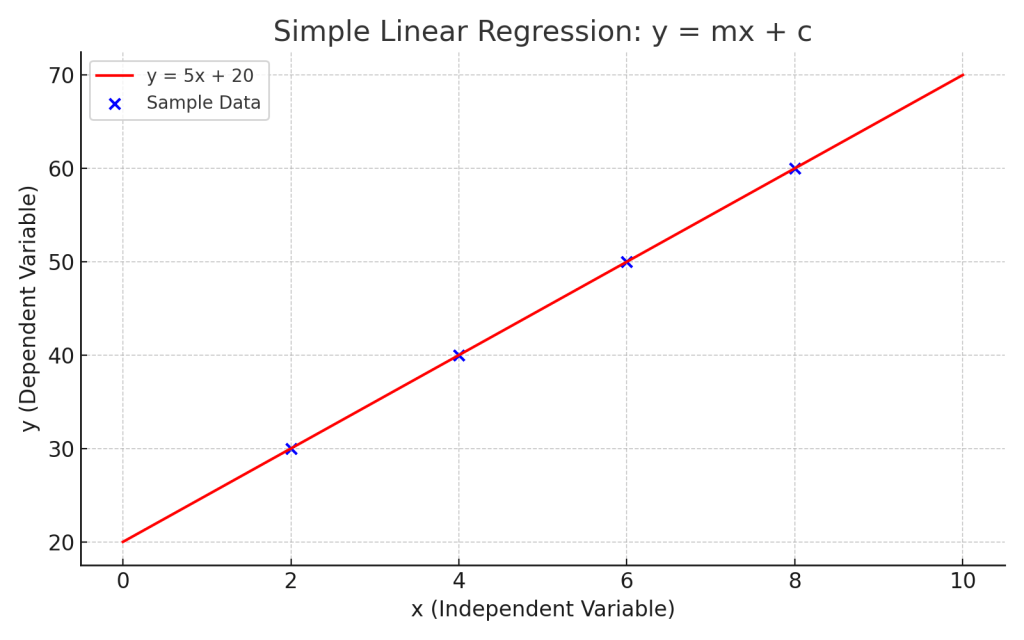
• 🔴 Red Line: The regression line defined by y=5x+20
• 🔵 Blue Dots: Sample data points showing how the line fits the data

How Does the Model Find the Best Line?

To learn the best values for m and c, the model uses a Loss Function. In Linear Regression, the most common loss function is the Mean Squared Error (MSE).

The formula for MSE is:

MSE = (1/n) × Σ(actual – predicted)²

This function calculates the average of the squared differences between actual values and predicted values. The model tries to minimize this error to find the best-fit line.

Multiple Linear Regression

When more than one input feature affects the outcome, we use Multiple Linear Regression. The equation becomes:

y = b₀ + b₁x₁ + b₂x₂ + … + bₙxₙ

For example, predicting house price using area, number of bedrooms, and location involves multiple variables.

Python Implementation Example

Using Python and scikit-learn, here’s how Linear Regression can be implemented:

from sklearn.linear_model import LinearRegression
import pandas as pd

data = {‘Hours’: [2, 4, 6, 8], ‘Marks’: [40, 50, 65, 80]}
df = pd.DataFrame(data)

model = LinearRegression()
model.fit(df[[‘Hours’]], df[‘Marks’])

predicted = model.predict([[5]])
print(“Predicted marks for 5 hours:”, predicted[0])

When to Use Linear Regression

– When your target is a numeric value

– When there is a linear relationship between features and target

– When the data is relatively clean and not full of extreme outliers

Limitations

– Assumes linearity in data

– Can be sensitive to outliers

– Multicollinearity between features can reduce performance

Linear Regression is a simple yet powerful algorithm in machine learning. It provides clear insights and accurate predictions when used with the right kind of data. Understanding how the loss function works and how to apply it in Python builds a strong foundation for more advanced algorithms.

Disclaimer: All information provided on www.academicbrainsolutions.com is for general educational purposes only. While we strive to provide accurate and up-to-date information, we make no representations or warranties of any kind, express or implied, about the completeness, accuracy, reliability, suitability, or availability of the information contained on the blog/website for any purpose. Any reliance you place on such information is therefore strictly at your own risk. The information provided on www.academicbrainsolutions.com is not intended to be a substitute for professional educational advice, diagnosis, or treatment. Always seek the advice of your qualified educational institution, teacher, or other qualified professional with any questions you may have regarding a particular subject or educational matter. In no event will we be liable for any loss or damage including without limitation, indirect or consequential loss or damage, or any loss or damage whatsoever arising from loss of data or profits arising out of, or in connection with, the use of this blog/website. Our blog/website may contain links to external websites that are not provided or maintained by us. We do not guarantee the accuracy, relevance, timeliness, or completeness of any information on these external websites. Comments are welcome and encouraged on www.academicbrainsolutions.com is but please note that we reserve the right to edit or delete any comments submitted to this blog/website without notice due to: Comments deemed to be spam or questionable spam, Comments including profanity, Comments containing language or concepts that could be deemed offensive, Comments that attack a person individually.By using www.academicbrainsolutions.com you hereby consent to our disclaimer and agree to its terms. This disclaimer is subject to change at any time without prior notice